¿Cómo medirías 12 minutos, si sólo dispones de un reloj de arena de 15 minutos y otro de 9 minutos?
Solución pasatiempo anterior:
Este problema se podría interpretar de dos formas distintas. Tal vez, para quitar ambigüedad, podrían haber aclarado si la distancia se mide de la forma habitual, en línea recta (recuerda que, al fin y al cabo, las moscas pueden volar), o las moscas quieren saber la distancia que tienen que recorrer andando sobre la superficie de la caja.
La posición en la que han de colocarse las moscas es, probablemente, la misma en ambos casos, pero la distancia a calcular no lo es. Si tratamos de alejar las moscas al máximo acabarán en las dos esquinas opuestas de la caja, eso es evidente.
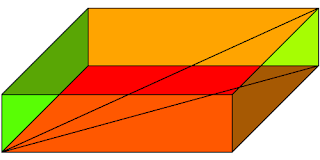
Si queremos medir la distancia en línea recta, hemos de imaginar la diagonal de la caja y usarla para dibujar un triángulo rectángulo al que podamos aplicar el teorema de Pitágoras. Vemos en el dibujo una manera de hacerlo (hay otras). Uno de los catetos de este triángulo es conocido, pero el otro es una diagonal de una cara, y también deberemos calcular su tamaño, ya que de nuevo será la hipotenusa de un triángulo rectángulo formado por los lados de la cara.
Al final, la longitud buscada, al cuadrado, será la suma de los tres cuadrados, 80, 60 y 20, es decir, 6400 + 3600 + 400 = 100*104. Su raíz cuadrada, evidentemente, no es exacta, tendrá la expresión 10*√104, aproximadamente 101,980390272.
Si, por el contrario, queremos la distancia más grande siguiendo la superficie de la caja, hemos de pensar en posibles despliegues de la caja, y en qué camino seguiría una mosca para llegar a la otra. También en este caso está claro que el lugar más lejano sería en dos esquinas opuestas de la caja, sólo que hay varios caminos para llega de una mosca a otra, según cómo despleguemos la caja (es decir, según qué caras recorra una mosca para buscar a la otra). Si recorremos un par de caras u otro, puede variar la longitud. Tenemos tres posibilidades, básicamente se trata de trazar la diagonal de un rectángulo, es decir, la hipotenusa de un triángulo rectángulo, por ejemplo, del rectángulo formado por dos de las caras de la caja al desplegarse.
En un caso, podría ser calcular la raíz de la suma de los cuadrados de 80 y de 60 más 20, es decir, de 12800, que son 10*√128, aproximadamente 113,13708499. En otro, la raíz de los cuadrados de 60 y de 80 más 20, es decir, de 13600, es decir, 10*√136, que obviamente sería más grande (aproximadamente 116,619037897). La última posibilidad sería tomar la raíz de la suma de los cuadrados de 20 y de 80 más 60, es decir, la raíz de 20000, o 10*√200, mucho mayor (aproximadamente 141,421356237).


No hay comentarios:
Publicar un comentario